5. Windowed Value Difference Metric (WVDM)

The IVDM algorithm can be thought of as sampling the value of Pa,u,c at the midpoint mida,u of each discretized range u. P is sampled by first finding the instances that have a value for attribute a in the range mida,u +/- wa / 2. Na,u is incremented once for each such instance, and Na,u,c is also incremented for each instance whose output class is c, after which Pa,u,c = Na,u,c / Na,u is computed. IVDM then interpolates between these sampled points to provide a continuous but rough approximation to the function pa,c(x). It is possible to sample P at more points and thus provide a closer approximation to the function pa,c(x), which may in turn provide for more accurate distance measurements between values.

Figure 9 shows pseudo-code for the Windowed Value Difference Metric (WVDM). The WVDM samples the value of Pa,x,c at each value x occurring in the training set for each attribute a, instead of only at the midpoints of each range. In fact, the discretized ranges are not even used by WVDM on continuous attributes, except to determine an appropriate window width, wa, which is the same as the range width used in DVDM and IVDM.

For each value x occurring in the training set for attribute a, P is sampled by finding the instances that have a value for attribute a in the range x +/- wa / 2, and then computing Na,x, Na,x,c, and Pa,x,c = Na,x,c / Na,x as before. Thus, instead of having a fixed number s of sampling points, a window of instances, centered on each training instance, is used for determining the probability at a given point. This technique is similar in concept to shifted histogram estimators (Rosenblatt, 1956) and to Parzen window techniques (Parzen, 1962).


Figure 9. Pseudo code for the WVDM learning algorithm.

For each attribute the values are sorted (using an O(nlogn) sorting algorithm) so as to allow a sliding window to be used and thus collect the needed statistics in O(n) time for each attribute. The sorted order is retained for each attribute so that a binary search can be performed in O(log n) time during generalization.

Values occurring between the sampled points are interpolated just as in IVDM, except that there are now many more points available, so a new value will be interpolated between two closer, more precise values than with IVDM.

The pseudo-code for the interpolation algorithm is given in Figure 10. This algorithm takes a value x for attribute a and returns a vector of C probability values Pa,x,c for c=1..C. It first does a binary search to find the two consecutive instances in the sorted list of instances for attribute a that surround x. The probability for each class is then interpolated between that stored for each of these two surrounding instances. (The exceptions noted in parenthesis handle outlying values by interpolating towards 0 as is done in IVDM.)


Figure 10. Pseudo-code for the WVDM probability interpolation (see Figure 9 for definitions).

Once the probability values for each of an input vector's attribute values are computed, they can be used in the vdm function just as the discrete probability values are.

The WVDM distance function is defined as:

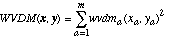(25)

and wvdma is defined as:

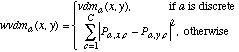(26)

[See erratum. There should be a square root over the summation in Equation (26).]
where Pa,x,c is the interpolated probability value for the continuous value x as computed in Figure 10. Note that we are typically finding the distance between a new input vector and an instance in the training set. Since the instances in the training set were used to define the probability at each of their attribute values, the binary search and interpolation is unnecessary for training instances because they can immediately recall their stored probability values, unless pruning techniques have been used.

One drawback to this approach is the increased storage needed to retain C probability values for each attribute value in the training set. Execution time is not significantly increased over IVDM or DVDM. (See Section 6.2 for a discussion on efficiency considerations).

Figure 11. Example of the WVDM probability landscape.

Figure 11 shows the probability values for each of the three classes for the first attribute of the Iris database again, this time using the windowed sampling technique. Comparing Figure 11 with Figure 8 reveals that on this attribute IVDM provides approximately the same overall shape, but misses much of the detail. For example, the peak occurring for output class 2 at approximately sepal length=5.75. In Figure 8 there is a flat line which misses this peak entirely, due mostly to the somewhat arbitrary position of the midpoints at which the probability values are sampled.

Table 7 summarizes the results of testing the WVDM algorithm on the same datasets as DVDM and IVDM. A bold entry again indicates the highest of the two accuracy measurements, and an asterisk (*) indicates a difference that is statistically significant at the 90% confidence level, using a two-tailed paired t-test.

Table 7. Generalization accuracy of WVDM vs. DVDM.

On this set of databases, WVDM was an average of 1.6% more accurate than DVDM overall. WVDM had a higher average accuracy than DVDM on 23 out of the 34 databases, and was significantly higher on 9, while DVDM was only higher on 11 databases, and none of those differences were statistically significant.

Section 6 provides further comparisons of WVDM with other distance functions, including IVDM.

Next: Section 6. Empirical Comparisons and Analysis of Distance Functions.

Return to Contents

Send comments to randy@axon.cs.byu.edu